EJERCICIOS INFORMÁTICA
1ª) ¿Qué sistema de numeración utilizan los ordenadores para codificar la información a su lenguaje?¿Qué números utiliza?
2ª) Pasa de decimal a binario el número 125
3ª) Pasa de binario a decimal el número 1011
4ª) ¿Qué código es el que utilizan normalmente los ordenadores para convertir un número binario en una letra o en un carácter?
5ª) ¿Qué es un bit?
6ª) ¿Qué es un byte?
7ª) ¿Cuál es la unidad de almacenamiento en informática?
8ª) ¿Cuántos bytes son 1MB? ¿Y cuantos bits?
9ª) ¿Cuántos MB son 1TB?
10ª) Nombra las 4 etapas en las que se puede dividir el funcionamiento de un ordenador.
11ª) ¿Qué son los periféricos?¿Cuantos tipos hay?
12ª) ¿Qué se conoce como “procesar información”?
13ª) ¿Qué es el microprocesador?
14ª) ¿En qué dos partes se divide el microprocesador?
15ª) Explica los datos que determinan el rendimiento de un microprocesador.
16ª) ¿Qué es la memoria RAM? Nombra los 4 tipos que existen.
17ª) ¿De qué valores suelen ser los módulos de memoria RAM?
18ª) ¿Qué es la memoria ROM o BIOS del sistema?
19ª) ¿Qué es la memoria caché? ¿Cuántas hay?
20ª) Ordena de mayor a menor capacidad de almacenamiento las siguientes unidades de almacenamiento: DVD, disquete, disco duro (HD), memoria flash y CD.
21ª) ¿Qué es la placa base de un ordenador?
22ª) Nombra los tipos de slots que conozcas.
23ª) ¿Qué es el chipset?
24-¿Qué es importante conocer de una fuente de alimentación?
25- A parte de la capacidad, que otra característica es importante en el disco duro:
26- Nombra los 5 puertos que existen por cable:
27-Nombra las 3 formas de conectar de forma inalámbrica:
28-¿Cuántos sectores constituyen un cluster normalmente?
29-Nombra dos tipos de monitores diferentes:
30- ¿Qué es la frecuencia de refresco de un monitor?.¿En qué monitores se usa?
31- ¿En qué monitores se usa el tiempo de refresco?
32- ¿Qué significa y qué es el dot pitch?
33- ¿Qué monitores trabajan con una resolución fija por que si no se pierde calidad?
34- ¿Qué significa RTB?
35- Pon las capacidades de almacenamiento que tienen: un disquete, un CD-ROM y un
DVD
36-¿Qué significan los siguientes números en una grabadora de DVD? 54x24x52x
37-¿Qué es un DVD dual?
38-¿Cuántas tipos de impresoras existen?
39-¿Cómo se llaman las tarjetas usadas para conexiones bluethoot?
40-Saca una flecha de cada componente de la placa base de la figura que conozcas y pon su nombre
solucion
1:el sistema orinarioen matemáticas e informática, es un sistema de numeración en el que los números se representan utilizando solamente las cifras cero y uno (0 y 1). Es el que se utiliza en las computadoras, debido a que trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).
2:Conversión entre binario y decimal
[editar] Decimal a binario
Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2. Es decir, cuando el número a dividir sea 1 finaliza la división.
A continuación se ordenan los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división, se les da la vuelta. Éste será el número binario que buscamos.Transformar el número decimal 131 en binario. El método es muy simple:
Ejemplo
131 dividido entre 2 da 65 y el resto es igual a 1 65 dividido entre 2 da 32 y el resto es igual a 1 32 dividido entre 2 da 16 y el resto es igual a 0 16 dividido entre 2 da 8 y el resto es igual a 0 8 dividido entre 2 da 4 y el resto es igual a 0 4 dividido entre 2 da 2 y el resto es igual a 0 2 dividido entre 2 da 1 y el resto es igual a 0 1 dividido entre 2 da 0 y el resto es igual a 1 -> Ordenamos los restos, del último al primero: 10000011
En sistema binario, 131 se escribe 10000011
Transformar el número decimal 100 en binario.
Ejemplo
Otra forma de conversión consiste en un método parecido a la factorización en números primos. Es relativamente fácil dividir cualquier número entre 2. Este método consiste también en divisiones sucesivas. Dependiendo de si el número es par o impar, colocaremos un cero o un uno en la columna de la derecha. Si es impar, le restaremos uno y seguiremos dividiendo entre dos, hasta llegar a 1. Después sólo nos queda tomar el último resultado de la columna izquierda (que siempre será 1) y todos los de la columna de la derecha y ordenar los dígitos de abajo a arriba.
Ejemplo
100|0 50|0 25|1 --> 1, 25-1=24 y seguimos dividiendo por 2 12|0 6|0 3|1 1|1 -->

Existe un último método denominado de distribución. Consiste en distribuir los unos necesarios entre las potencias sucesivas de 2 de modo que su suma resulte ser el número decimal a convertir. Sea por ejemplo el número 151, para el que se necesitarán las 8 primeras potencias de 2, ya que la siguiente, 28=256, es superior al número a convertir. Se comienza poniendo un 1 en 128, por lo que aún faltarán 23, 151-128 = 23, para llegar al 151. Este valor se conseguirá distribuyendo unos entre las potencias cuya suma dé el resultado buscado y poniendo ceros en el resto. En el ejemplo resultan ser las potencias 4, 2, 1 y 0, esto es, 16, 4, 2 y 1, respectivamente.
Ejemplo
20= 1|1 21= 2|0 22= 4|0 23= 8|0 24= 16|0 25= 32|0 26= 64|0 27= 128|0

[editar] Decimal (con decimales) a binario
Para transformar un número del sistema decimal al sistema binario:
Se transforma la parte entera a binario. (Si la parte entera es 0 en binario será 0, si la parte entera es 1 en binario será 1, si la parte entera es 5 en binario será 101 y así sucesivamente).
Se sigue con la parte fraccionaria, multiplicando cada número por 2. Si el resultado obtenido es mayor o igual a 1 se anota como un uno (1) binario. Si es menor que 1 se anota como un 0 binario. (Por ejemplo, al multiplicar 0.6 por 2 obtenemos como resultado 1.2 lo cual indica que nuestro resultado es un uno (1) en binario, solo se toma la parte entera del resultado).
Después de realizar cada multiplicación, se colocan los números obtenidos en el orden de su obtención.
Algunos números se transforman en dígitos periódicos, por ejemplo: el 0.1.
Ejemplo
0,3125 (decimal) => 0,0101 (binario).Proceso: 0,3125 · 2 = 0,625 => 00,625 · 2 = 1,25 => 10,25 · 2 = 0,5 => 0 0,5 · 2 = 1 => 1 En orden: 0101 -> 0,0101 (binario)
Ejemplo
0,1 (decimal) => 0,0 0011 0011 ... (binario). Proceso: 0,1 · 2 = 0,2 ==> 00,2 · 2 = 0,4 ==> 00,4 · 2 = 0,8 ==> 0 0,8 · 2 = 1,6 ==> 10,6 · 2 = 1,2 ==> 1 0,2 · 2 = 0,4 ==> 0 <--se repiten las cuatro cifras, periódicamente 0,4 · 2 = 0,8 ==> 0 <-0,8 · 2 = 1,6 ==> 1 <- 0,6 · 2 = 1,2 ==> 1 <- ... En orden: 0 0011 0011 ... => 0,0 0011 0011 ... (binario periódico)
Ejemplo
5.5 = 5,55,5 (decimal) => 101,1 (binario).Proceso: 5 => 1010,5 · 2 = 1 => 1 En orden: 1 (un sólo dígito fraccionario) -> 101,1 (binario)
Ejemplo
6,83 (decimal) => 110,110101000111 (binario). Proceso:6 => 1100,83 · 2 = 1,66 => 10,66 · 2 = 1,32 => 1 0,32 · 2 = 0,64 => 00,64 · 2 = 1,28 => 10,28 · 2 = 0,56 => 0 0,56 · 2 = 1,12 => 10,12 · 2 = 0,24 => 00,24 · 2 = 0,48 => 0 0,48 · 2 = 0,96 => 00,96 · 2 = 1,92 => 10,92 · 2 = 1,84 => 1 0,84 · 2 = 1,68 => 1En orden: 110101000111 (binario) Parte entera: 110 (binario) Encadenando parte entera y fraccionaria: 110,110101000111 (binario)
[editar] Binario a decimal
Para realizar la conversión de binario a decimal, realice lo siguiente:
Inicie por el lado derecho del número en binario, cada cifra multiplíquela por 2 elevado a la potencia consecutiva (comenzando por la potencia 0, 20).
Después de realizar cada una de las multiplicaciones, sume todas y el número resultante será el equivalente al sistema decimal.
Ejemplos:
(Los números de arriba indican la potencia a la que hay que elevar 2)



También se puede optar por utilizar los valores que presenta cada posición del número binario a ser transformado, comenzando de derecha a izquierda, y sumando los valores de las posiciones que tienen un 1.
Ejemplo
El número binario 1010010 corresponde en decimal al 82. Se puede representar de la siguiente manera:

entonces se suman los números 64, 16 y 2:

Para cambiar de binario con decimales a decimal se hace exactamente igual, salvo que la posición cero (en la que el dos es elevado a la cero) es la que está a la izquierda de la coma y se cuenta hacia la derecha a partir de -1:

[editar] Binario a decimal (con parte fraccionaria binaria)
1. Inicie por el lado izquierdo (la primera cifra a la derecha de la coma), cada número multiplíquelo por 2 elevado a la potencia consecutiva a la inversa (comenzando por la potencia -1, 2-1).
2.Después de realizar cada una de las multiplicaciones, sume todas y el número resultante será el equivalente al sistema decimal.
Ejemplos
0,101001 (binario) = 0,640625(decimal). Proceso:
1 · 2 elevado a -1 = 0,50 · 2 elevado a -2 = 0 1 · 2 elevado a -3 = 0,1250 · 2 elevado a -4 = 00 · 2 elevado a -5 = 0 1 · 2 elevado a -6 = 0,015625La suma es: 0,640625
0.110111 (binario) = 0,859375(decimal). Proceso:
1 · 2 elevado a -1 = 0,51 · 2 elevado a -2 = 0,25 0 · 2 elevado a -3 = 01 · 2 elevado a -4 = 0,06251 · 2 elevado a -5 = 0,03125 1 · 2 elevado a -6 = 0,015625La suma es: 0,859375
[editar] Operaciones con números binarios
[editar] Suma de números binarios
La tabla de sumar para números binarios es la siguiente:
+
0
1
0
0
1
1
1
10
Las posibles combinaciones al sumar dos bits son:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Note que al sumar 1 + 1 es 102, es decir, llevamos 1 a la siguiente posición de la izquierda (acarreo). Esto es equivalente, en el sistema decimal a sumar 9 + 1, que da 10: cero en la posición que estamos sumando y un 1 de acarreo a la siguiente posición.
Ejemplo
1 10011000 + 00010101 ——————————— 10101101
Se puede convertir la operación binaria en una operación decimal, resolver la decimal, y después transformar el resultado en un (número) binario. Operamos como en el sistema decimal: comenzamos a sumar desde la derecha, en nuestro ejemplo, 1 + 1 = 10, entonces escribimos 0 en la fila del resultado y llevamos 1 (este "1" se llama acarreo o arrastre). A continuación se suma el acarreo a la siguiente columna: 1 + 0 + 0 = 1, y seguimos hasta terminar todas la columnas (exactamente como en decimal).
[editar] Resta de números binarios
El algoritmo de la resta en sistema binario es el mismo que en el sistema decimal. Pero conviene repasar la operación de restar en decimal para comprender la operación binaria, que es más sencilla. Los términos que intervienen en la resta se llaman minuendo, sustraendo y diferencia.
Las restas básicas 0 - 0, 1 - 0 y 1 - 1 son evidentes:
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1 (se transforma en 10 - 1 = 1) (en sistema decimal equivale a 2 - 1 = 1)
La resta 0 - 1 se resuelve igual que en el sistema decimal, tomando una unidad prestada de la posición siguiente: 0 - 1 = 1 y me llevo 1, lo que equivale a decir en el sistema decimal, 2 - 1 = 1.
Ejemplos
10001 11011001 -01010 -10101011 —————— ————————— 00111 00101110
En sistema decimal sería: 17 - 10 = 7 y 217 - 171 = 46.
Para simplificar las restas y reducir la posibilidad de cometer errores hay varios métodos:
Dividir los números largos en grupos. En el siguiente ejemplo, vemos cómo se divide una resta larga en tres restas cortas:
100110011101 1001 1001 1101 -010101110010 -0101 -0111 -0010 ————————————— = ————— ————— ————— 010000101011 0100 0010 1011
Utilizando el complemento a dos (C2). La resta de dos números binarios puede obtenerse sumando al minuendo el «complemento a dos» del sustraendo.
Ejemplo
La siguiente resta, 91 - 46 = 45, en binario es:
1011011 1011011 -0101110 el C2 de 0101110 es 1010010 +1010010 ———————— ———————— 0101101 10101101
En el resultado nos sobra un bit, que se desborda por la izquierda. Pero, como el número resultante no puede ser más largo que el minuendo, el bit sobrante se desprecia.
Un último ejemplo: vamos a restar 219 - 23 = 196, directamente y utilizando el complemento a dos:
11011011 11011011 -00010111 el C2 de 00010111 es 11101001 +11101001 ————————— ————————— 11000100 111000100
Y, despreciando el bit que se desborda por la izquierda, llegamos al resultado correcto: 11000100 en binario, 196 en decimal.
Utilizando el complemento a uno. La resta de dos números binarios puede obtenerse sumando al minuendo el complemento a uno del sustraendo y a su vez sumarle el bit que se desborda.
[editar] Producto de números binarios
La tabla de multiplicar para números binarios es la siguiente:
·
0
1
0
0
0
1
0
1
El algoritmo del producto en binario es igual que en números decimales; aunque se lleva a cabo con más sencillez, ya que el 0 multiplicado por cualquier número da 0, y el 1 es el elemento neutro del producto.
Por ejemplo, multipliquemos 10110 por 1001:
10110 1001 ————————— 10110 00000 00000 10110 ————————— 11000110
En sistemas electrónicos, donde suelen usarse números mayores, se utiliza el método llamado algoritmo de Booth.
11101111 111011 __________ 11101111 11101111 00000000 11101111 11101111 11101111 ______________ 11011100010101
[editar] División de números binarios
La división en binario es similar a la decimal; la única diferencia es que a la hora de hacer las restas, dentro de ladivisión, éstas deben ser realizadas en binario.
Ejemplo
Dividir 100010010 (274) entre 1101 (13):
100010010 |1101 ——————-0000 010101 ——————— 10001 -1101——————— 01000 - 0000 ——————— 10000 - 1101 ——————— 00111 - 0000 ——————— 01110 - 1101 ——————— 00001
[editar] Conversión entre sistema binario y octal
[editar] Sistema Binario a octal
Debido a que el sistema octal tiene como base 8, que es la tercera potencia de 2, y que dos es la base del sistema binario, es posible establecer un método directo para convertir de la base dos a la base ocho, sin tener que convertir de binario a decimal y luego de decimal a octal. Este método se describe a continuación:
Para realizar la conversión de binario a octal, realice lo siguiente:
1) Agrupe la cantidad binaria en grupos de 3 en 3 iniciando por el lado derecho. Si al terminar de agrupar no completa 3 dígitos, entonces agregue ceros a la izquierda.
2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:
Número en binario
000
001
010
011
100
101
110
111
Número en octal
0
1
2
3
4
5
6
7
3) La cantidad correspondiente en octal se agrupa de izquierda a derecha.
Ejemplos
110111 (binario) = 67 (octal). Proceso:
111 = 7110 = 6Agrupe de izquierda a derecha: 67
11001111 (binario) = 317 (octal). Proceso:
111 = 7001 = 1 11 entonces agregue un cero, con lo que se obtiene 011 = 3 Agrupe de izquierda a derecha: 317
1000011 (binario) = 103 (octal). Proceso:
011 = 3000 = 01 entonces agregue 001 = 1 Agrupe de izquierda a derecha: 103
Si el número binario tiene parte decimal, se agrupa de tres en tres desde el punto decimal hacia la derecha siguiendo los mismos criterios establecidos anteriormente para números enteros. Por ejemplo:
0.01101 (binario) = 0.32 (octal) Proceso: 011 = 3 01 entonces agrege 010 = 2 Agrupe de izquierda a derecha: 32 Agrege la parte entera: 0.32
[editar] Octal a binario
Cada dígito octal se convierte en su binario equivalente de 3 bits y se juntan en el mismo orden.
Ejemplo
247 (octal) = 010100111 (binario). El 2 en binario es 10, pero en binario de 3 bits es Oc(2) = B(010); el Oc(4) = B(100) y el Oc(7) = (111), luego el número en binario será 010100111.
[editar] Conversión entre binario y hexadecimal
[editar] Binario a hexadecimal
Para realizar la conversión de binario a hexadecimal, realice lo siguiente:
1) Agrupe la cantidad binaria en grupos de 4 en 4 iniciando por el lado derecho. Si al terminar de agrupar no completa 4 dígitos, entonces agregue ceros a la izquierda.
2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:
Número en binario
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Número en hexadecimal
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
3) La cantidad correspondiente en hexadecimal se agrupa de derecha a izquierda.
Ejemplos
110111010 (binario) = 1BA (hexadecimal). Proceso:
1010 = A1011 = B1 entonces agregue 0001 = 1 Agrupe de derecha a izquierda: 1BA
11011110101 (binario) = 6F5 (hexadecimal). Proceso:
0101 = 51111 = F110 entonces agregue 0110 = 6 Agrupe de derecha a izquierda: 6F5
[editar] Hexadecimal a binario
Note que para pasar de Hexadecimal a binario, se remplaza el número Hexadecimal por el equivalente de 4 bits, de forma similar a como se hace de octal a binario.
] Tabla de conversión entre decimal, binario, hexadecimal, octal, BCD, Exceso 3 y Código Gray o Reflejado
Decimal
Binario
Hexadecimal
Octal
BCD
Exceso 3
Gray o Reflejado
0
0000
0
0
0000
0011
0000
1
0001
1
1
0001
0100
0001
2
0010
2
2
0010
0101
0011
3
0011
3
3
0011
0110
0010
4
0100
4
4
0100
0111
0110
5
0101
5
5
0101
1000
0111
6
0110
6
6
0110
1001
0101
7
0111
7
7
0111
1010
0100
8
1000
8
10
1000
1011
1100
9
1001
9
11
1001
1100
1101
10
1010
A
12
0001 0000
1111
11
1011
B
13
0001 0001
1110
12
1100
C
14
0001 0010
1010
13
1101
D
15
0001 0011
1011
14
1110
E
16
0001 0100
1001
15
1111
F
17
0001 0101
1000
3:Decimal (con decimales) a binario
Para transformar un número del sistema decimal al sistema binario:
Se transforma la parte entera a binario. (Si la parte entera es 0 en binario será 0, si la parte entera es 1 en binario será 1, si la parte entera es 5 en binario será 101 y así sucesivamente).
Se sigue con la parte fraccionaria, multiplicando cada número por 2. Si el resultado obtenido es mayor o igual a 1 se anota como un uno (1) binario. Si es menor que 1 se anota como un 0 binario. (Por ejemplo, al multiplicar 0.6 por 2 obtenemos como resultado 1.2 lo cual indica que nuestro resultado es un uno (1) en binario, solo se toma la parte entera del resultado).
Después de realizar cada multiplicación, se colocan los números obtenidos en el orden de su obtención.
Algunos números se transforman en dígitos periódicos, por ejemplo: el 0.1.
Ejemplo
0,3125 (decimal) => 0,0101 (binario).Proceso: 0,3125 · 2 = 0,625 => 00,625 · 2 = 1,25 => 10,25 · 2 = 0,5 => 0 0,5 · 2 = 1 => 1 En orden: 0101 -> 0,0101 (binario)
Ejemplo
0,1 (decimal) => 0,0 0011 0011 ... (binario). Proceso: 0,1 · 2 = 0,2 ==> 00,2 · 2 = 0,4 ==> 00,4 · 2 = 0,8 ==> 0 0,8 · 2 = 1,6 ==> 10,6 · 2 = 1,2 ==> 1 0,2 · 2 = 0,4 ==> 0 <--se repiten las cuatro cifras, periódicamente 0,4 · 2 = 0,8 ==> 0 <-0,8 · 2 = 1,6 ==> 1 <- 0,6 · 2 = 1,2 ==> 1 <- ... En orden: 0 0011 0011 ... => 0,0 0011 0011 ... (binario periódico)
4:
El antiguo matemático hindú Pingala presentó la primera descripción que se conoce de un sistema de numeración binario en el siglo tercero antes de nuestra era, lo cual coincidió con su descubrimiento del concepto del número cero.
Una serie completa de 8 trigramas y 64 hexagramas (análogos a 3 bit) y números binarios de 6 bit eran conocidos en la antigua China en el texto clásico del I Ching. Series similares de combinaciones binarias también han sido utilizadas en sistemas de adivinación tradicionales africanos, como el Ifá, así como en la geomancia medieval occidental.
Un arreglo binario ordenado de los hexagramas del I Ching, representando la secuencia decimal de 0 a 63, y un método para generar el mismo fue desarrollado por el erudito y filósofo Chino Shao Yong en el siglo XI.
En 1605 Francis Bacon habló de un sistema por el cual las letras del alfabeto podrían reducirse a secuencias de dígitos binarios, las cuales podrían ser codificadas como variaciones apenas visibles en la fuente de cualquier texto arbitrario.
El sistema binario moderno fue documentado en su totalidad por Leibniz, en el siglo XVII, en su artículo "Explication de l'Arithmétique Binaire". En él se mencionan los símbolos binarios usados por matemáticos chinos. Leibniz utilizó el 0 y el 1, al igual que el sistema de numeración binario actual.
En 1854, el matemático británico George Boole publicó un artículo que marcó un antes y un después, detallando un sistema de lógica que terminaría denominándose Álgebra de Boole. Dicho sistema desempeñaría un papel fundamental en el desarrollo del sistema binario actual, particularmente en el desarrollo de circuitos electrónicos.
5:1. Funcionamiento de un ordenador
Como hemos podido ver en otros módulos del curso, un ordenador está compuesto por dos tipos de componentes, por un lado está el software (programas) y por otro el hardware (componentes físicos). La parte hardware de la máquina está compuesta por un conjunto de circuitos electrónicos utilizados para procesar la información digital. Esta información puede expresarse en forma de dos valores (1 si hay corriente y 0 si no la hay). En la práctica se utilizan los dígitos 0 y 1 para codificar y operar con esta información digital, lo que se conoce como sistema binario.
1.1 Codificación binaria
La información digital se representa a través del sistema binario, con valores 0 y 1 respectivamente. Las imágenes, sonidos, letras, etc deben convertirse en 0's y 1's para que el ordenador pueda procesarlas. A ese proceso de conversión se llama digitalización.
Para utilizar el sistema binario hay que utilizar únicamente los dígitos 0 y 1 por lo que después del 1 viene el 10, que es el siguiente número que sólo utiliza el 0 y el 1. A cada uno de los dígitos que componen un número binario se le denomina bit. Así por ejemplo, para almacenar el número 19, el ordenador utilizaría el 10011
6:
Bit es el acrónimo Binary digit. (dígito binario). Un bit es un dígito del sistema de numeración binario.
Mientras que en el sistema de numeración decimal se usan diez dígitos, en el binario se usan sólo dos dígitos, el 0 y el 1. Un bit o dígito binario puede representar uno de esos dos valores, 0 ó 1.
Se puede imaginar un bit, como una bombilla que puede estar en uno de los siguientes dos estados:
El bit es la unidad mínima de información empleada en informática, en cualquier dispositivo digital, o en la teoría de la información. Con él, podemos representar dos valores cuales quiera, como verdadero o falso, abierto o cerrado, blanco o negro, norte o sur, masculino o femenino, rojo o azul, etc. Basta con asignar uno de esos valores al estado de "apagado" (0), y el otro al estado de "encendido" (1).
Memoria de computadora de 1980 donde se pueden ver los bits físicos. Este conjunto de unos 4x4 cm. corresponden a 512 bytes.
7:
En los dispositivos de almacenamiento del computador, se almacenan en forma temporal o permanentemente losprogramas y datos que son manejados por las aplicaciones que se ejecutan en estos sistemas.
Debido a la cantidad de información que es manejada actualmente por los usuarios, los dispositivos de almacenamiento se han vuelto casi tan importantes como el computador. Aunque actualmente existen dispositivos para almacenar que superan los 650 MB de memoria; no es suficiente por la falta de capacidad para transportar losdocumentos y hacer reserva de la información más importante.
Es por tal razón que hoy en día existen diferentes dispositivos de almacenamiento, que tienen su propia tecnología. En la presente investigación se estudiaran todos y cada uno de los dispositivos de almacenamiento de un computador, las distintas marcas, clasificación, entre otros puntos que se irán desarrollando a medida que se avanza en la investigación.
Los sistemas informáticos pueden almacenar los datos tanto interna (en la memoria) como externamente (en los dispositivos de almacenamiento). Internamente, las instrucciones o datos pueden almacenarse por un tiempo en los chips de silicio de la RAM (memoria de acceso aleatorio) montados directamente en la placa de circuitos principal de lacomputadora, o bien en chips montados en tarjetas periféricas conectadas a la placa de circuitos principal del ordenador. Estos chips de RAM constan de conmutadores sensibles a los cambios de la corriente eléctrica, esto quiere decir que los datos son almacenados por tiempo limitado (hasta que dejamos de suministrar energía eléctrica) por esta razón aparecen los dispositivos de almacenamiento secundarios o auxiliares, los cuales son capaces de conservar la información de manera permanente, mientras su estado físico sea óptimo. Los dispositivos de almacenamiento externo pueden residir dentro del CPU y están fuera de la placa de circuito principal. [1]
Los Dispositivos de Almacenamiento se pueden clasificar de acuerdo al modo de acceso a los datos que contienen:
- Acceso secuencial: En el acceso secuencial, el elemento de lectura del dispositivo debe pasar por el espacio ocupado por la totalidad de los datos almacenados previamente al espacio ocupado físicamente por los datos almacenados que componen el conjunto de información a la que se desea acceder.
- Acceso aleatorio: En el modo de acceso aleatorio, el elemento de lectura accede directamente a la direccióndonde se encuentra almacenada físicamente la información que se desea localizar sin tener que pasar previamente por la almacenada entre el principio de la superficie de grabación y el punto donde se almacena la información buscada.
- Memoria ROM: Esta memoria es sólo de lectura, y sirve para almacenar el programa básico de iniciación, instalado desde fábrica. Este programa entra en función en cuanto es encendida la computadora y su primer función es la de reconocer los dispositivos, (incluyendo memoria de trabajo), dispositivos.
8:1 Byte son 8 Bits.
1 Kbyte son 1024 Bytes
1 Mbyte son 1024 Kbyes
1 Gbytes son 1024 Mbytes
1 Terabyte son 1024 Gbytes
9:Kb = kilobytes
Mb=megabytes
Gb= gigabytes
Tb= terabyte
9: bit = 1 byte
1024 bytes = 1 Kb
1024 Kb = 1 Mb
1024 Mb = 1 Gb
1024 Gb = 1 Tb
1 Tb = 1 073 741 824 kb.
1 Tb = 1024 Gb.
1 Kilobyte = 1024 bytes
1 Megabyte= 1024 Kbytes
1Gigabyte= 1024 Mbytes
1Terabyte= 1024 Gbytes10:
Las WebQuest y el Uso de la InformaciónPor lo extenso del tema y con el fin de poder tratarlo en profundidad, hemos decidido dividir en tres entregas el cubrimiento de las etapas finales de los modelos diseñados para desarrollar la Competencia en el Manejo de la Información (CMI). Por lo tanto, la presente es la cuarta entrega de las siete que le dedicaremos a este importante "megatema". En esta ocasión nos enfocaremos en el uso de la información mediante la aplicación de las WebQuests. La próxima edición estará dedicada a las herramientas de aprendizaje visual y en junio nos referiremos a la síntesis y la evaluación para completar así el cubrimiento de todas las partes del modelo para CMI. La última entrega sobre CMI tratará los límites de Internet como fuente de información.11:Periféricos de entrada de información: Son los elementos a través de los que se introduce información a la computadora. Ej.: teclado, ratón (o mouse), scanner, lápiz óptico, lector de código de barras, lector de tarjeta magnética, tableta digitalizadora.
Periféricos de entrada/salida de la información: Son subsistemas que permiten a la computadora almacenar temporal o indefinidamente la información o los programas en los soportes de información (tales como: disco rígido, disco flexible o diskette, disco compacto, DVD, cinta magnética, etc ).
Periféricos de salida de la información: Son los periféricos que trasmiten los resultados obtenidos tras el procesamiento de la información por la computadora al exterior del sistema informático para que pueda ser utilizado por los seres humanos u otros sistemas diferentes. Ej: plotter, parlante, impresora, fax, pantalla.
Periféricos de comunicación: Estos subsitemas están dedicados a permitir la conexión de la computadora con otros subsistemas informáticos a través de diversos medios. El medio más común es la línea telefónica. El periférico de comunicación más utilizado es el módem (modulador-demodulador). Ej.: módems, placas de red, etc.11: Al hablar de las teorías del procesamiento de información en este articulo nos remitimos algunas descripciones teóricas entre ellas la teoría computacional en relación con la conocida maquina de turing, a su vez basados enprincipios matemáticos y conjuga varias ramas de las matemáticas. la teoría cibernética Esta teoría tuvo una influencia central en el modo de pensar sobre la conducta humanan ya que permitió introducir la teleología, las causas finales dentro del análisis científico y finalmente lo que recientemente se habla la teoría por simulación de computadora.
Esta ultima hace énfasis a que un operador es aquel que resuelva el problema, así mismo el papel del psicólogo en la simulación por computadora es definir con precisión la estrategia para la generación de movimiento, que hace énfasis en el pensamiento como selección de respuestas.
12:
El microprocesador (o simplemente procesador) es el circuito integrado central y más complejo de un sistema informático; a modo de ilustración, se le suele asociar por analogía como el «cerebro» de un computador. Es uncircuito integrado constituido por millones de componentes electrónicos. Constituye la unidad central de procesamiento (CPU) de un PC catalogado como microcomputador.
Es el encargado de ejecutar los programas; desde el sistema operativo hasta las aplicaciones de usuario; sólo ejecutainstrucciones programadas en lenguaje de bajo nivel, realizando operaciones aritméticas y lógicas simples, tales comosumar, restar, multiplicar, dividir, las lógicas binarias y accesos a memoria.
Esta unidad central de procesamiento está constituida, esencialmente, por registros, una unidad de control, unaunidad aritmético lógica (ALU) y una unidad de cálculo en coma flotante(conocida antiguamente como «co-procesador matemático»).
El microprocesador está conectado, generalmente, mediante un zócalo específico a la placa base de la computadora. Normalmente, para su correcto y estable funcionamiento, se le adosa un sistema de refrigeración, que consta de undisipador de calor fabricado en algún material de alta conductividad térmica, como cobre o aluminio, y de uno o másventiladores que fuerzan la expulsión del calor absorbido por el disipador; entre éste último y la cápsula del microprocesador suele colocarse pasta térmica para mejorar la conductividad térmica. Existen otros métodos más eficaces, como la refrigeración líquida o el uso de células peltier para refrigeración extrema, aunque estas técnicas se utilizan casi exclusivamente para aplicaciones especiales, tales como en las prácticas de overclocking.
La medición del rendimiento de un microprocesador es una tarea compleja, dado que existen diferentes tipos de "cargas" que pueden ser procesadas con diferente efectividad por procesadores de la misma gama. Una métrica del rendimiento es la frecuencia de reloj que permite comparar procesadores con núcleos de la misma familia, siendo este un indicador muy limitado dada la gran variedad de diseños con los cuales se comercializan los procesadores de una misma marca y referencia. Un sistema informático de alto rendimiento puede estar equipado con varios microprocesadores trabajando en paralelo, y un microprocesador puede, a su vez, estar constituido por variosnúcleos físicos o lógicos. Un núcleo físico se refiere a una porción interna del microprocesador cuasi-independiente que realiza todas las actividades de una CPU solitaria, un núcleo lógico es la simulación de un núcleo físico a fin de repartir de manera más eficiente el procesamiento. Existe una tendencia de integrar el mayor número de elementos dentro del propio procesador, aumentando así su eficiencia energética y la miniaturización. Entre los elementos integrados están las unidades de punto flotante, controladores de la memoria RAM, controladores de buses y procesadores dedicados de video.
13:La Cpu o unidad central de proceso, es el cerebro de la computadora y se encuentra ubicado específicamente en el microprocesador. Posee dos componentes, la Unidad de Control y la Unidad aritmético-lógica. La Unidad de Control es la parte de la CPU que controla a la aritmético lógica y a la memoria principal. La Unidad Aritmético Lógica es un circuito digital utilizado para el cálculo de operaciones aritméticas y- 0
Add a comme
lunes, 26 de marzo de 2012
Suscribirse a:
Enviar comentarios (Atom)


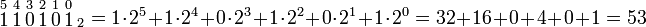






Add a comment